به منظور بیان کمی آسیب پذیری اجزای مختلف سازه ای و یا غیر سازه ای بر حسب میزان خطر زلزله می توان در مورد هر نوع از سازه ها یا اجزای غیر سازه ای حساس به جابجایی نسبی و اجزای غیر سازه ای حساس به شتاب، احتمال وقوع یا فرا گذشت از یک میزان خسارت خاص را بر حسب یک ویژگی معرف زلزله نظیر PGA , PGV, PGD بیان نمود. تکرار این عملیات برای مقادیر مختلف PGA یا سایر تک پارامترها، منجر به تولید منحنی های نرمال شده ای موسوم به منحنی شکنندگی (Fragility curve) میگردد.
در مورد تاریخچه مطالعاتی درباره منحنی های شکنندگی باید اشاره کرد رسم و تولید منحنی های شکنندگی از سازه های تأسیسات هسته ای آغاز شد، چرا که این سازه ها جزء سازه های بسیار مهم و آسیب دیدگی آنها در هنگام زمین لرزه بسیار خطر ناک است. در سال 1980 منحنی های شکنندگی برای نیروگاه های هسته ای رسم شد]16[. رسم این منحنی ها با استفاده از عوامل شکنندگی چون فشار آب، مقاومت بتن، جابجایی و تنش ایجاد شده در پوسته های مخازن براساس سطوح مختلف PGA صورت گرفت.
سپس، این منحنی ها توسط " کرچرومارتین" در سال 1993کمی توسعه داده شد. ]17[ ، این منحنی ها از لحاظ محاسباتی بسیار ساده تا حدی ابتدایی بودند و تنها بصورت تجربی و با کمک قضاوت مهندسی تهیه شده بودند، در این مقاله نیز محور قائم احتمال وقوع و محور افقی مقدار کیفی جنبش زمین بودند، از این منحنی ها جهت برآورد خسارت لرزه ای ساختمان ها استفاده شد.
می توان گفت که بعد از زمین لرزه ی نورثریج (1994) توجه بیشتری به تخمین میزان خسارت سازه ها شد، و مهندسین توجه بیشتری به پیش بینی میزان خسارت مالی سازه ها در زلزله های شدید نشان دادند.
در سال 1994 طی مطالعه ای بر سازه های ایالت کالیفرنیا، از ظوابط ATC-13 برای رسم منحنی های شکنندگی استفاده شد]19[. در آن تحقیق، منحنی های شکنندگی برای سازه های چوبی، فولادی قاب خمشی و بتن مسلح (40 سازه) رسم شد.
آنانوس و همکاران در سال 1995] 20[، مطالعات بیشتری بر مبنای توزیع بار مندرج در ATC انجام دادند و مدل جدیدی از منحنی شکنندگی را ارائه دادند در این مقاله تمامی محاسبات لرزه ای بر مبنای ATC-13 انجام گردید و این بار، محور افقی مقادیری از مرکالی اصلاح شده بود که حالت علمی تری برای آنالیز شکنندگی محسوب می شد و تابع توزیع احتمالاتی به صورت نرمال فرض شده بود و ایده های مناسبی برای پیشنهاد جهت استفاده از رکورد زلزله در این منحنی جهت کارهای آینده ارائه داده شد.
منحنی های شکست، خرابی را بین حالات ناچیز، متوسط، سنگین و کامل توزیع می کنند، این منحنی ها که می توانند به صورت نمودار نیز نشان داده شوند برای هر، حالت خرابی در هر جنبش زمین جداگانه رسم می شوند و به عنوان ورودی در جریان محاسبه خسارت سازه ای وارد می شوند
برای نشان دادن احتمال شرطی، تجاوز پاسخ لرزه ای سازه (R) از حالات حدی عملکردی خاصی (ترک خوردگی، تسلیم، جابجایی، شکاف، کمانش و فروریزش) که به Performance Limit Stateمعروفند و با بیان می شود و وابسته به پارامتر معرف زمین لرزه ، I می باشد، از فرمول 2-1 استفاده می گردد که توسط Corvera و Barron درسال 2000 ارئه شده است: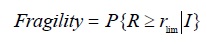
R: (پارامتر پاسخ (تغییرشکل ، نیرو، سرعت و ...
r min : حد آستانه پاسخ، که با خرابی همبسته شده است
I: پارامتر معرف زمین لرزه (دوره باز گشتMMI ، PGA)
این تعریف برای پارامتر های N بعدی نیز قابل تعمیم است :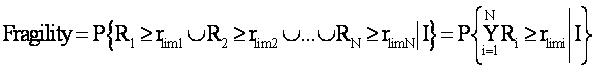
اگر رابطه بالا را برای حالت دو بعدی ،شتاب و جابجایی تعریف کنیم، داریم: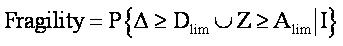
: Δمتغیر پیشای پاسخ جابجایی
: Zمتغیر پیشای پاسخ شتاب
Dlim: حد آستانه جابه جایی
: Alimحد آستانه شتاب
در این حالت پاسخ به صورت یک سطح زنگ مانند (Bell surface) در فضای شبه شتاب طیفی وجابجایی طیفی نشان داده می شود. زمانیکه تجاوز ازحالات حدی مشخص شود، با منحنی های شکست نشان داده می شود.
بطور کلی برای بدست آوردن منحنی های شکنندگی 4 روش وجود دارد:
1- روش تجربی (Empirical method)
2- بر اساس قضاوت مهندسی (Judgemental approach)
3- روش تحلیلی (Analytical method)
4- روش ترکیبی (Hybrid approach)
1-روش تجربی
این روش بر اساس مشاهدات خرابی سازه ها در زلزله های گذشته عمل می کند و اگر تمام جزئیات و تأثیرات اندر کنش خاک- سازه، توپوگرافی، خصوصیات چشمه لرزه ای و فاصله تا ساختگاه، در نظر گرفته شوند، در کارهای عملی روشی قابل اعتماد است، اما به دلیل مربوط بودن این اطلاعات به یک موقعیت و منطقه خاص و همچنین کم بودن داده های زلزله های گذشته در مناطق پر جمعیت، کاربرد منحنی های تولید شده به این روش محدود می باشد .
- فواید استفاده از این روش
الف-برای ساختمانهای قدیمی که با اصول مهندسی ساخته نشده اند و تخمین آسیب پذیری آنها با مدل کردن امکان پذیر نیست، کاربرد دارد.
ب-خسارت واقعی وارد شده بر اجزای سازه ای وغیر سازه ای در یک منطقه را نشان می دهد.
ج-مودهای واقعی شکست را در نظر می گیرد.
د-روش استفاده ازآن آسان است و فرضیات کمی دارد.
-محدودیت های روش
الف-به دلیل تغییر سازه ها در اثر باز سازی نسبت به زمانیکه زلزله رخ داده است،تخمین شدت زمین لرزه دشوار است.
ب-پارامترهای بالقوه خسارت را به خوبی در نظر نمی گیرد.
ج-امکان مدلسازی صحیح اندر کنش خاک – سازه و جنبش زمین دشوار است.
د-اعمال این روش به سازه های جدید و یا اصلاح شده دشوار می باشد.
2- روش قضاوت مهندسی
منحنی های تولید شده به این روش مثل منحنی هایFEMA/NIBS و ATC- 13، براساس اطلاعات کارشناسان بدست می آیند. این روش تحت تأثیر محدودیتهایی که کمیت وکیفیت آمارهای خسارت سازه ای را مد نظر قرار می دهد، نمی باشد، قابل اعتماد بودن این منحنی ها زیاد کمی نیست و بستگی به تجربه فردی کارشناس و طبیعت منطقه ای روابط بدست آمده دارد، واگر نتوان از روشهای دیگر استفاده نمود، این روش انتخاب می شود.
3- روش تحلیلی
بر اساس تحلیل مدلهای مختلف که طبق آیین نامه های لرزه ای طراحی شده اند و تحت شدتهای افزاینده زمین لرزه، پایگاه داده های آماری برای رسم منحنی ها بدست می آید. با افزایش تعداد تحلیلهای انجام شده ، درصد خطا کاهش یافته و منحنی هایی با درصد اطمینان بالاتر نسبت به دو حالت قبل بدست می آید، این تحلیل ها می توانند به صورت تحلیل تاریخچه زمانی غیر خطی، تحلیل طیفی خطی و تحلیل استاتیکی غیر خطی باشند.
فواید روش:
الف-نتایج وابسته به جنبش شدید زمین(ورودی) می باشد
ب-به سازه هایی اعمال می گردد که قبلاً آسیب ندیده اند.
ج-اندرکنش بین سازه – خاک و جنبش شدید زمین را در بر می گیرد.
د-از شدت زمین لرزه استفاده نمی گردد.
محدودیت های روش:
الف-ساختار ویژه و فرضیات پیچیده ای دارد.
ب-یک مکانیزم فروریزش و خرابی ویژه را در بر می گیرد.
ج-بر اساس داده های واقعی خسارت نیست.
د-جنبه های دقیق معماری، دیوارهای پرکننده تأثیر زیادی بر رفتار مدل می گذارد که در این روش در نظر گرفته نمی شود.
توصیه می شود که منحنی های بدست آمده از تحلیل با نتایج زلزله های واقعی کالیبره شوند، وبرای در نظر گرفتن تعداد بیشتر سازه، اختصاص مدلهای پاسخ ساده شده روش مناسبی می باشد چرا که کاربرد روشهای تحلیلی به دلیل مراحل محاسباتی وقت گیر، محدود می باشد.
4- روش ترکیبی
این روش برای متعادل کردن کمبود اطلاعات مشاهده ای (تجربی) روش دوم و کم کردن خطاهای مدل کردن در روش سوم، از طریق جمع آوری اطلاعات از منابع مختلف استفاده می شود. روش ترکیبی منحنی های شکنندگی قابل اعتمادی را با ترکیب ارزیابی های ریاضی و داده های خسارت مشاهده شده از سازه ها در زلزله های قبل تولید می کند. اساس روش، استفاده از مدلهای تحلیلی برای تکمیل اطلاعات بدست آمده از بررسیهای آماری است .منحنی هایی که از روشهای متفاوت ذکر شده بدست می آیند در منابع مورد نیاز تولید ودقت نتایج با یکدیگر متفاوتند و انتخاب استفاده از هر یک از روش ها با در نظر گرفتن دقت درنتایج و یا حجم عملیات صورت می گیرد.
توزیع نرمال، یکی از مهمترین توزیع های آماری است.نمودار این توزیع که به منحنی نرمال معروف است، حالت زنگی شکل داشته و بیشتر وقایعی که در طبیعت و تحقیقات علمی بوقوع می پیوندد از این منحنی پیروی می کند، منحنی نرمال را منحنی گوس هم می نامند (شکل زیر منحنی تابع توزیع نرمال را نشان می دهد )
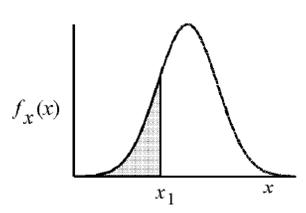
متغیر تصادفی X که منحنی توزیع آن زنگی شکل باشد را متغیر تصادفی نرمال می نامیم.
تابع چگالی این توزیع بصورت زیر می باشد.
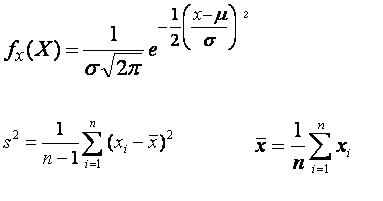
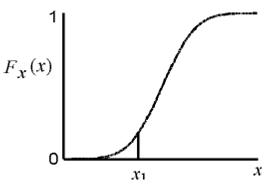
برای بدست آوردن مقدار احتمال یک توزیع نرمال از مساحت سطح زیر منحنی نرمال استفاده می کنند. که به آن تابع توزیع تجمعی نرمال می گویند(شکل زیر).
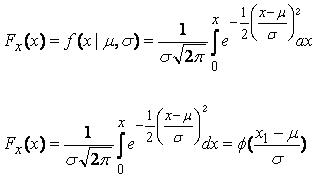
تولید منحنی شکنندگی
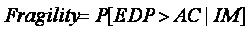
در رابطه بالاIM شدت زلزله است.که معمولا برابرشتاب حداکثر زمین(PGA) فرض می شود، EDP پارامتر تقاضای مهندسی است، که از خروجی تحلیل های دینامیکی غیر خطی بدست می آید وAC شرایط قابل قبول مربوط به حالت حدی مفروض است.
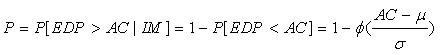
یک توزیع نرمال آماری برای هر پارامتر تقاضای مهندسی ( EDP) در هر شدت حرکت زلزله(IM) در نظر گرفته می شود.برای ارزیابی احتمال تجاوزاز یک حد مرزی خاص(AC)، میانگین و انحراف معیار هر یک از EDPها برای اثر مجموع نگاشت های زلزله محاسبه می شود.سپس با استفاده ازتابع توزیع تجمعی توزیع نرمال، احتمال تجاوز هر یک از EDP ها از حالت حدی داده شده محاسبه می شود .
دقت منحنی های شکنندگی
شناخت عوامل ایجاد خطا مهمترین گام در امر افزایش دقت منحنی های شکنندگی است، عوامل موثر در ایجاد خطا در منحنی های شکنندگی عبارتند از:
1) کمبود اطلاعات موجود.
2) وجود اطلاعات نادرست یا کم دقت.
3) خطا در عملیات ریاضی.
مساله اساسی دیگری که در خلال روند تهیه منحنی های شکنندگی باید به آن دقت نمود استفاده از یک روش ریاضی منطقی برای تلفیق داده های آماری با یکدیگر می باشد. توجه لازم باید به این نکته معطوف گردد که داده های مختلفی که از زلزله های گذشته و یا مطالعات عددی آزمایشگاهی بدست آمده اند از حیث دقت در یک سطح نمی باشد، لذا باید در خلال انجام تحلیل های آماری به داده های مختلف بر حسب میزان دقت آنها وزن داده شود.
در مجموع برای تعیین منحنی های شکنندگی سازه ها به منظور افزایش دقت محاسبات، بهتر است برای حالت خاص سازه از نظر شرایط هندسی، شرایط تکیه گاهی و شرایط ساختگاهی یک منحنی شکنندگی خاص برای هر حالت تخریب بدست آید.
یکی دیگر از روش هایی که می توان با استفاده از آن منحنی های شکنندگی را ترسیم کرد شاخص خرابی می باشد.
پارک – انگ و ون در سال 1985 با استفاده از رابطه معروف شاخص خسارت پارک-انگ روشی در جهت طراحی سازه ها ارائه دادند. در این روش عمده ترین پارامترهای اولیه طرح، برش پایه و شاخص شدت زمین لرزه است که بر اساس آن شکل پذیری سازه به دست می آید]42[.
سطوح خرابی و شاخص های خرابی
هنگامیکه سازه ها تحت بار زلزله قرار می گیرند حالت های خرابی متعددی اتفاق می افتد.
- خرابی غیر سازه ای
2- خرابی سازه ای کم
3- خرابی سازه ای متوسط
4- خرابی سازه ای زیاد
5- فروپاشی کلی
این حالت های خرابی با استفاده از شاخص خرابی پیشنهاد شده توسط پارک و انگ تعریف می شوند. شاخص خرابی پارک و انگ برای المان های سازه ای به صورت زیر تعریف می شود:
(2 27)
〖DI〗_PA=(Ф_m-Ф_y)/(Ф_u-Ф_y )+β_e/(M_u Ф_u ) ∫▒dE
Ф_m: حداکثر خمش ایجاد شده توسط زلزله
Ф_y: خمش تسلیم
Ф_u: تغییر شکل نهایی تحت بار یکنواخت
dE ʃ : انرژی جذب شده تجمعی
My : ممان تسلیم
eβ : ضریب مربوط به نوع سازه
برای کاهش مقاومت اسمی، پارک و همکارانش مقدار1/0=β را پیشنهاد کرده اند. با استفاده از این مدل سه شاخص آسیب محاسبه می شود.
شاخص آسیب المان : تیرها و ستون ها
شاخص آسیب طبقه : اجزای افقی و قائم و آسیب کل طبقه
آسیب کل ساختمان
به عبارت دیگر در این مدل میزان خسارت به صورت تجمعی در کلیه اعضاء ، طبقات و کل سازه در نظر گرفته می شود.
منحنی شکنندگی و ماتریس خرابی
احتمال PFij که احتمال فراگذشت سطح خرابی i ام برای زلزله ای با حداکثر شتاب PGA معادل aj به صورت زیر بدست می آید:
(2 28)
PF=Prob(DT ≥〖DT〗_i│PGA=a_j)=F_DT (〖DT〗_i |PGA=a_j)
DTi= شاخص خرابی مربوط به i امین سطح خرابی
FDT= تابع توزیع احتمال شاخص خرابی
با در نظر گرفتن توزیع لوگ نرمال برای DTi و PFij داریم:
( )Ф : تابع توزیع نرمال
: میانگین لگاریتم طبیعی شاخص خرابی است
: انحراف معیار لگاریتم شاخص خرابی
ماتریس خرابی نشان دهنده احتمال وقوع یک آسیب در سطح خرابی مشخصی است. احتمال PDSij، نشان دهنده خرابی یک سازه به علت زمین لرزه ای با شتاب حداکثر aj در سطح خرابی i ام است که می توان با استفاده از داده های منحنی شکنندگی به صورت زیر محاسبه کرد:
تولید منحنی های شکنندگی با استفاده از شاخص خرابی
یکی دیگر از روش هایی که می توان با استفاده از آن منحنی های شکنندگی را ترسیم کرد شاخص خرابی می باشد.
پارک – انگ و ون در سال 1985 با استفاده از رابطه معروف شاخص خسارت پارک-انگ روشی در جهت طراحی سازه ها ارائه دادند. در این روش عمده ترین پارامترهای اولیه طرح، برش پایه و شاخص شدت زمین لرزه است که بر اساس آن شکل پذیری سازه به دست می آید]42[.
سطوح خرابی و شاخص های خرابی
هنگامیکه سازه ها تحت بار زلزله قرار می گیرند حالت های خرابی متعددی اتفاق می افتد.
- خرابی غیر سازه ای
2- خرابی سازه ای کم
3- خرابی سازه ای متوسط
4- خرابی سازه ای زیاد
5- فروپاشی کلی
این حالت های خرابی با استفاده از شاخص خرابی پیشنهاد شده توسط پارک و انگ تعریف می شوند. شاخص خرابی پارک و انگ برای المان های سازه ای به صورت زیر تعریف می شود:
(2 27)
〖DI〗_PA=(Ф_m-Ф_y)/(Ф_u-Ф_y )+β_e/(M_u Ф_u ) ∫▒dE
Ф_m: حداکثر خمش ایجاد شده توسط زلزله
Ф_y: خمش تسلیم
Ф_u: تغییر شکل نهایی تحت بار یکنواخت
dE ʃ : انرژی جذب شده تجمعی
My : ممان تسلیم
eβ : ضریب مربوط به نوع سازه
برای کاهش مقاومت اسمی، پارک و همکارانش مقدار1/0=β را پیشنهاد کرده اند. با استفاده از این مدل سه شاخص آسیب محاسبه می شود.
شاخص آسیب المان : تیرها و ستون ها
شاخص آسیب طبقه : اجزای افقی و قائم و آسیب کل طبقه
آسیب کل ساختمان
به عبارت دیگر در این مدل میزان خسارت به صورت تجمعی در کلیه اعضاء ، طبقات و کل سازه در نظر گرفته می شود.
منحنی شکنندگی و ماتریس خرابی
احتمال PFij که احتمال فراگذشت سطح خرابی i ام برای زلزله ای با حداکثر شتاب PGA معادل aj به صورت زیر بدست می آید:
(2 28)
PF=Prob(DT ≥〖DT〗_i│PGA=a_j)=F_DT (〖DT〗_i |PGA=a_j)
DTi= شاخص خرابی مربوط به i امین سطح خرابی
FDT= تابع توزیع احتمال شاخص خرابی
با در نظر گرفتن توزیع لوگ نرمال برای DTi و PFij داریم:
( )Ф : تابع توزیع نرمال
: میانگین لگاریتم طبیعی شاخص خرابی است
: انحراف معیار لگاریتم شاخص خرابی
ماتریس خرابی نشان دهنده احتمال وقوع یک آسیب در سطح خرابی مشخصی است. احتمال PDSij، نشان دهنده خرابی یک سازه به علت زمین لرزه ای با شتاب حداکثر aj در سطح خرابی i ام است که می توان با استفاده از داده های منحنی شکنندگی به صورت زیر محاسبه کرد:
http://ieea.ir/


